Frequency Response
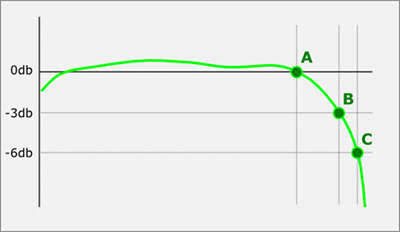
Figure 1: use this calculator to estimate the high frequency performance of Your design. This is a pure theoretical basic model and results are approximate.
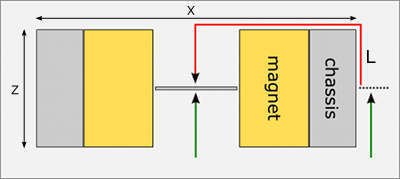
Figure 2: a ribbon microphone motor, view from above. The green line shows the path of a sound wave before it gets delayed by the chassis. The red line (L) shows the length of the vawe's path to the backside of the ribbon. The sound wave travels the half-thickness of the motor twice and a half-width once, so the approximate length of the path can be calculated using formula: L = Z + X/2, where Z is the thickness of a motor and X is its width (measured in the middle of the height if the width is not constant, f.ex. if the motor has a sand-clock shape).
| * Point A: | roll-off start |
| * Point B: | 3 db signal drop |
| * Point C: | 6 db signal drop |
So, why and how does the profile of a motor affects the frequency response? The answer is in phase shifting of a sound wave. The simplest way to understand the phase is to consider it as a displacement of one wave in relation to other wave. When the sound wave moves through the air it both attenuates and continuously changes phase in relation to some fixed points. Ribbon microphones are mostly designed as pressure-gradient microphones. Diaphragm (ribbon in our case) of a pressure-gradient microphone gets motivated by the pressure difference between the front and the back of the diaphragm.
As it takes some finite time for a wave to travel across the motor assembly, it attenuates and its phase shifts on the way. The proportion of these changes varies with frequency. Low frequency waves are very long, measured in meters (100 Hz wave is 3.43 meters or 11.25 feet long), so the proportion of wave's displacement during the travel around the motor in relation to its wavelength is very small, but on the other hand, the energy of a low frequency wave is huge, so even a smallest change in phase will cause a significant difference in pressure on both sides of a ribbon, thus displacing it. High frequency waves carry very low energy, but they are short, measured in centimeters (5 kHz wave is 6.86 cm or 2.70 inches long), so while the motive force is low, the proportion of the distance around the motor is significant in relation to the wavelength, so phase shift will be big and proportional pressure difference between sides of ribbon will be much higher still providing enough energy to displace the foil. Everything is very smart in nature, isn't it?
Physics engineers may throw rock at me, but for better understanding I would roughly say, that the force, that moves the ribbon is in some way equal to the phase difference between front and back multiplied by the energy of a wave (ribbon motion = phase shift * wave energy). Low frequency waves carry huge energy, but the phase shift is very small, on the other hand, high frequency waves carry very small energy, but phase shift if huge, so the part of frequency band dynamically equalizes this way.
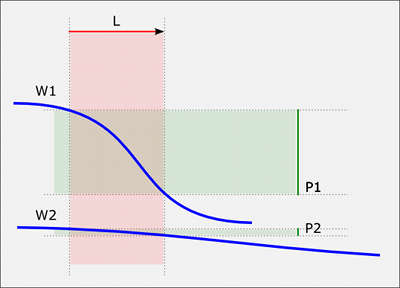
Figure 3: the dependence of phase shift from wavelength over a given distance. Red line (L) is the length of the path from the front to the back of a ribbon (see figure 2).
| * L: | the length of a sound path |
| * W1: | high frequency wave |
| * W2: | low frequency wave |
| * P1: | HF phase shift |
| * P2: | LF phase shift |
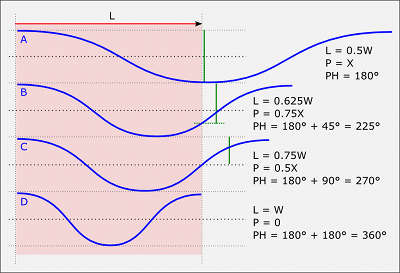
Figure 4: L - sound path lenght (see figure 2); W - wavelength; P - pressure difference between the front and the back of a ribbon (green lines), where X = maximum relative pressure difference; PH - phase shift between the front and the back of a ribbon.
High Frequency Performance
The response remains flat until the phase shift reaches 180 degrees (half of the wavelength), the point, where the high pressure pushes the ribbon from the front and at the same time it gets sucked in by low pressure from the back, giving the highest possible relative pressure difference between sides. After this point the rear pressure starts raising again, thus reducing the difference and the motive force with it.
The point of total zero is reached, when the wave makes a full cycle between front and back, as the pressure on both sides becomes virtually the same at the moment. So, the frequency when the wavelength becomes equal to the length of the path from the front to the back of the ribbon is our high-end zero point. In case of motors, that are offered on this site, the length of the path is 14 mm, so the termination frequency is 24.5 kHz. But, in fact, this is not the number, which is interesting for us, because the actual roll-off starts far beyond that point. After the point of 180 degree phase shift, additional shift by 45 degrees (1/8 of wavelength) will cause the signal level drop by 3 db (which is the standard threshold in defining the frequency response of a microphone) and after another 45 degrees (90 in total) the signal will drop by another 3 db (6 db in total, meaning voltage drop by 50%). In case of same 14 mm path the 3 db drop point should be at 15.3 kHz and 6db drop point at 18.3 kHz, with the flat response until 180 degree point at 12.3 kHz.
To make math more clear (see figure 4): the 180 degree point (the end of flat part of response) is the half (4/8) of the wavelength, so we have to find out the frequency with the wavelength of twice the sound path length. For example, if we have the wave path length of 20 mm, the response will be flat until the wavelength reaches 40 mm, which is equivalent to 8.6 kHz. The 3 db drop point is located at 5/8 of the wavelength (180 degrees is 4/8 + 45 degrees, which is 1/8 = 5/8), so the signal will drop by 3 db, when the the sound path length is 5/8 or 0.625 of the wavelength. We have to divide the path length by 0.625. With 20 mm path length it is 20/0.625 = 32 mm, which is equivalent to 10.7 kHz. Thus, we can define, that the ribbon microphone with the length of sound path of 20 mm will have the frequency response up to 10.7 kHz before -3 db output signal drop.
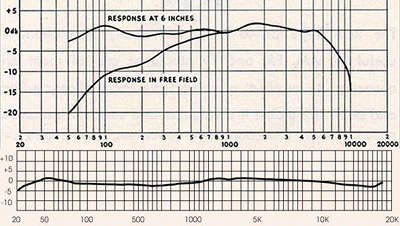
Figure 5: the comparison of frequency responses of classical (above) and modern (below) ribbon microphones. RCA SK-46 and Royer R-121 as examples. Significant path length reduction resulted in much wider and flatter response.







